A formal proof of the Chip Model Channel Separation Property
Thomas Hallgren,
Programatica Meeting, 2004-05-11
A formal proof of the Chip Model Channel Separation Property
Thomas Hallgren
Programatica Meeting, 2004-05-11
┌─────────┐ ┌─────────┐
───┤ pick ch ├───►┤ chip ├──►
└─────────┘ └─────────┘
| = |
┌─────────┐ ┌─────────┐
───┤ chip ├───►┤ pick ch ├──►
└─────────┘ └─────────┘
|
Warning
- This talk is about a manually constructed verification proof.
- In our HCSS04 paper, Dick Kieburtz wrote
The motivation to develop an automatic verification server lies in
the boring nature of verification proofs.
Unlike proofs of interesting mathematical theorems, many of which
are based upon deep insights into the underlying mathematical
structures, and which, once done, become the subject of continued
study and improvement, verification proofs tend to be based upon
shallow theories of superficially complex
structures. Such proofs may not require deep insight, although
they are often highly detailed.
- Be prepared to be bored!
Encouragement
- Even without automation, constructing this proof took a couple of days,
rather than a couple of weeks that some estimated.
- Perhaps the value of automation is overrated?
Remember the Curry-Howard isomorphism?
Proofs are programs!
- Programs are usually constructed manually.
How do we manage complexity in programs?
- We invent useful abstraction and construct libraries of reusable software
components.
- We use high-level languages with good abstraction mechanisms.
- We make use of program generators (automation) for certain specific tasks
(e.g. parsers).
Automation is always welcome!

The Chip
|
chip :: [Packet] → [Packet]
type Packet = (Channel,Data)
type Channel = Int
type Data = [Word]
|
┌──────┐
ps ───┤ chip ├──► ps'
└──────┘
|
- One chip processes packets on a number of independent channels
- Behavior:
- input a packet
- do some processing (encryption/decryption),
- output a modified packet
- Packet processing is stateful: the output for
a packet can depend on all previous input on the same channel.
Channel Separation Property
Property of interest:
channel separation
( = no information leaks between channels)
┌─────────┐ ┌─────────┐
──┤ chip ├──►┤ pick ch ├──►
└─────────┘ └─────────┘
| =
|
┌─────────┐ ┌─────────┐
──┤ pick ch ├──►┤ chip ├──►
└─────────┘ └─────────┘
|
assert Separation =
∀ ch . {pick ch . chip} === {chip . pick ch}
pick :: Channel → [Packet] → [Packet]
pick ch = filter ((==ch).fst)
A variant of the Channel Separation Property
┌──────┐
───┤ chip ├──►
└──────┘
| =
|
┌─────────┐ ┌─────────┐
┌─►┤ pick 1 ├──►┤ chip ├──┐
│ └─────────┘ └─────────┘ │
│ ┌─────────┐ ┌─────────┐ │
───┼─►┤ pick 2 ├──►┤ chip ├──┼──►
│ └─────────┘ └─────────┘ │
│ ... ... │
│ ┌─────────┐ ┌─────────┐ │
└─►┤ pick n ├──►┤ chip ├──┘
└─────────┘ └─────────┘
|
Processing all channels in one chip is the same as having one chip per channel.
Filling in the details
This is the actual main assertion.
chip :: Algs → ChipState → [Packet] → [Packet]
type Algs = Channel → Alg
type ChipState = (Memory,Regs)
type Regs = FM RegFile
assert Separation =
∀ algs . ∀ ch . ∀ state . ∀ ps .
{pick ch (chip algs state ps)}
=== {chip algs state (pick ch ps)}
The Chip Model
chip :: Algs → ChipState → [Packet] → [Packet]
chip algs state ps = fst (runS (manyPackets algs ps) state)
manyPackets :: Algs → [Packet] → StateM ChipState [Packet]
manyPackets algs = mapM (onePacket algs)
onePacket :: Algs → Packet → StateM ChipState Packet
onePacket algs (chan,ws) =
do regfile ← liftM (\regs→FM.lookup regs chan) (inSnd load)
(ws',regfile') ← inFst (doPacket (algs chan) ws regfile)
finishPacket chan ws' regfile'
doPacket :: Alg → Data → RegFile → StateM Memory (Data,RegFile)
doPacket alg ws regf = ...
For all the details, view the code with pfebrowser...
For reference...
Generic monadic operations
liftM :: Monad m ⇒ (a → b) → m a → m b
mapM :: Monad m ⇒ (a → m b) → [a] → m [b]
State monad operations
inFst :: StateM s1 a → StateM (s1,s2) a
inSnd :: StateM s2 a → StateM (s1,s2) a
runS :: StateM s a → s → (a,s)
Observations 1
Although the function
chip is defined monadically,
it is equivalent(*) to a simple list traversing function:
chip algs state [] = []
chip algs state (p:ps) = p':chip algs state' ps
where (p',state') = runS (onePacket algs p) state
Under the assumption that onePacket has the right properties,
we can prove Separation with induction over the input packet list,
without reasoning about monadic code.
(*) This equivalence follows directly from the definitions.
Observations 2
Even if the state argument is the same
on both sides of the equation we want to prove,
pick ch (chip algs state ps) === chip algs state (pick ch ps)
because of the filtering, they will be different
in the recursive calls, when we try to do a proof by induction.
Hence, the induction proof needs to be for a more general equation.
Observations 3
As we saw on a previous slide, packet processing is stateful.
- The
Memory is used only for temporary storage. Algorithms
can not keep data in memory for use when processing future packets.
- Each channel has its own register file, and the contents of registers
is preserved between packets.
Overall proof structure
The proof of
Separation is obtained by combining
the proofs of
CondSeparation,
AllGoodAlgs, and
SameState.
assert CondSeparation =
∀ algs ch state1 state2 ps .
GoodAlg {algs ch} ==>
Invariant state1 state2 ch ==>
{pick ch (chip algs state1 ps)}
=== {chip algs state2 (pick ch ps)}
assert AllGoodAlg = ∀ alg . GoodAlg alg
assert SameState =
∀ state . ∀ ch . Invariant state state ch
Good algorithms
assert AllGoodAlg = ∀ alg . GoodAlg alg
property GoodAlg =
{| alg | ∀ ws . ∀ regf .
StateIndependent {doPacket alg ws regf} |}
property StateIndependent =
{| m | ∀ s1 . ∀ s2 .
{fst (runS m s1)} === {fst (runS m s2)} |}
-
GoodAlgs makes sure that there are no information leaks through
the shared memory.
Invariant in the proof of CondSeparation
assert SameState =
∀ state . ∀ ch . Invariant state state ch
property Invariant =
{| state1, state2, ch |
{regfile ch state1} === {regfile ch state2} |}
regfile :: Channel → ChipState → RegFile
regfile ch state = FM.lookup (snd state) ch
-
Maintaining the
Invariant makes sure that there is no information
leaks through the register files.
CondSeparation proof outline
- Base case, ps = []: trivial, because LHS = RHS = []
- Induction step:
ps = (ch',ws):ps'
- Two cases
ch' == ch: the equation reduces to
ch' /= ch: the equation reduces to
Invariant in the proof of AllGoodAlg
Recall
assert AllGoodAlg = ∀ alg . GoodAlg alg
property GoodAlg =
{| alg | ∀ ws . ∀ regf .
StateIndependent {doPacket alg ws regf} |}
property StateIndependent =
{| m | ∀ s1 . ∀ s2 .
{fst (runS m s1)} === {fst (runS m s2)} |}
doPacket :: Alg → Data → RegFile → StateM Memory (Data,RegFile)
doPacket as a whole is completely state (Memory) independent.
- The steps that comprise
doPacket work on a packet stored in
memory, and can thus not be completely state independent.
- The invariant needs to capture that the algorithm only touches the part
of the memory where the packet is stored.
Invariant in the proof of AllGoodAlg, first attempt
- We would like to introduce the following definitions
(essentially the free theorem for the state monad):
property RelatedResult R =
{| r1,r2 | {fst r1}==={fst r2} /\ R {snd r1} {snd r2} |}
property MostlyStateIndependent R =
{| m | ∀ s1 . ∀ s2 .
R s1 s2 ==> RelatedResult R {runS m s1} {runS m s2} |}
assert ReturnS = ∀ x . ∀ R . MostlyStateIndependent R {return x}
assert BindS =
∀ m1 . ∀ xm2 . ∀ R .
MostlyStateIndependent R m1 ==>
(∀ x . MostlyStateIndependent R {xm2 x}) ==>
MostlyStateIndependent R {m1 >>= xm2}
- This is the way my first proof in Alfa was structured.
- But P-Logic is a first-order logic, so this is not allowed.
Invariant in the proof of AllGoodAlg, degeneralized
property EqRange r =
{| m1,m2 | ∀ a .
InRange r a ==> {lookupM m1 a} === {lookupM m2 a} |}
property RelatedResult range =
{| r1,r2 | {fst r1}==={fst r2}
/\ EqRange range {snd r1} {snd r2} |}
property MostlyStateIndependent range =
{| m | ∀ mem1 . ∀ mem2 .
EqRange range mem1 mem2 ==>
RelatedResult range {runS m mem1} {runS m mem2} |}
assert ReturnS_MSI =
∀ range . ∀ x . MostlyStateIndependent range {return x}
assert BindS_MSI =
∀m1 . ∀xm2 . ∀range .
MostlyStateIndependent range m1 ==>
(∀x . MostlyStateIndependent range {xm2 x}) ==>
MostlyStateIndependent range {m1 >>= xm2}
AllGoodAlg proof outline
- The previous slide showed that
>>= and return
preserve the MostlyStateIndependent property.
- The proof of
AllGoodAlgs consists of analogous proofs
that the other monadic operations used in the definition of
doPacket also preserve the MostlyStateIndependent
property.
- There are similar definitions for the protected memory monad.
What if?
- If the code was more polymorphic, would the free theorem for the type
of
doPacket be all we need?
Files
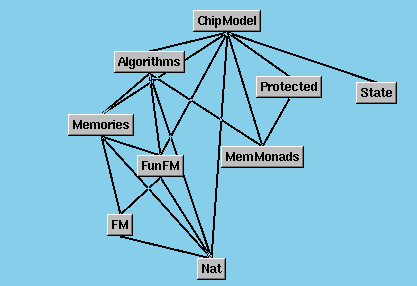
| Haskell module | Description
|
|---|
| Algorithms | Reg, RegFile, Code, Alg, runAlg
|
| ChipModel | The chip model and main property assertions
|
| Examples | A sample algorithm and a test case
|
| FM | class FM (finite maps) and definitions of expected properties
|
| FunFM | Functions from natural numbers as finite maps
|
| MemMonads | class MemMonad
|
| Memories | Memory, Addr, Word, Data, Range, ...
|
| Nat | Natural numbers
|
| Protected | Protected memory monad
|
| State | Implemenation of the State Monad
|
Imports from the Alfa library and other utilities
- Propositional logic: conjunction, implication
- Equality: subsitution, congruence, symmetry, transitivity
- Booleans: inference rules for if-then-else expressions and
boolean conjunction (
&&)
Maybe: inference rules for the function maybe.
- Natural numbers: addition, equality, order and related properties.
Random notes and concluding remarks
Readability of proofs?
- I used the most compact proof representation,
only the names of proof rules are visible (like a proof script in a tactical
theorem prover). Being familiar with the proof rules makes it easier
to understand the proof...
- Proof rules are just functions from libraries.
Everything is available for browsing in Alfa.
- Natural deduction style proofs would be more self-explanatory, easy to
obtain, but less practical since they would not fit on my screen.
Certificate machinery
Random notes
- No existential quantification was used.
- Being restricted to a first-order logic is frustrating,
and seems very unnatural to a functional programmer!
Some general, reusable properties of state monads could not be formulated,
so I had to resort to a a less modular solution.
(Suggestion: extend P-Logic syntax to higher-order logic. We don't expect
all proof tools to support every aspect of the logic anyway...)
- The code was not developed in accordance with "extreme formal methods"
approach advocated in the Programatica project ==> Program structure
and proofs more complicated than necessary.
Conjectures
- The operators
inFst and inSnd,
intended to provide
separation by types, have a very small role in the proof.
Eliminating them would simplify the model somewhat and not significantly
complicate the proof.
- The proof of
AllGoodAlgs depends on the memory
allocation function always returning address zero, but it would be
easy to change the protected memory monad to implement relative
addressing, thus preserving the separation property even when
packets are store at arbitrary locations in memory. This would
make it possible to prove separation for a more realistic,
concurrent chip model.
- There seems to be some other redundancy (unnecessary complications)
in the model. It seems possible to generalize and simplify it (and hence
the proofs). (The current model would just be a special case.)
- The proofs of
AllGoodAlgs and CondSeparation
have the same overall structure (bisimulation), so it should be possible
to simplify the proofs by factoring out some reusable parts.
Pointers
The code is in the Programatica CVS repository:
programatica/examples/ChannelSeparation/Alfa
- Chip model, properties and proofs expressed entirely in Alfa.
programatica/examples/ChannelSeparation/Alfa/Haskell
- Chip model in Haskell,
- properties expressed as P-Logic assertions,
- Alfa certificates associating proof in Alfa to the asserted properties.
The End
Questions?
Box drawing tests
┌─┐
│ │
└─┘
┌──────┐
───┤ chip ├───
└──────┘
┌─────────┐ ┌─────────┐ ┌─────────┐ ┌─────────┐
───┤ pick ch ├───▸┤ chip ├───►──┤ chip ├────┤ pick ch ├──►
└─────────┘ └─────────┘ └─────────┘ └─────────┘


