A formal proof of the Chip Model Channel Separation Property

Thomas Hallgren

Talk at the Programatica Review Meeting, 2004-09-16

   ┌─────────┐    ┌─────────┐
───┤ pick ch ├───►┤  chip   ├──►
   └─────────┘	  └─────────┘

   ┌─────────┐    ┌─────────┐
───┤  chip   ├───►┤ pick ch ├──►
   └─────────┘	  └─────────┘

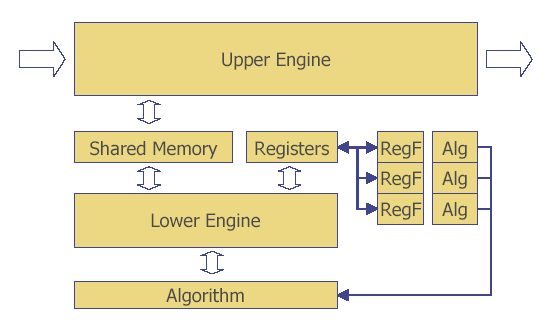
The Chip

A model of a cryptographic chip, loosely based on the AIM chip from Motorola.

Proof of the separation property

The chip model is expressed in Haskell.
Property assertions are expressed in P-logic embedded in the Haskell code.
The Programatica tools allow Haskell + P-logic to be translated into the language used by the proof assistant Alfa.
The proofs were constructed in Alfa and recorded in certificates attached to the P-logic assertion in the Haskell code.
We can currently only handle total functions over finite data structures with this approach. Fortunately, the Haskell code for the chip model falls in this category.

The Chip Model in Haskell

chip :: [Packet] → [Packet] type Packet = (Channel,Data) type Channel = Int type Data = [Word]

      ┌──────┐
ps ───┤ chip ├──►  ps'
      └──────┘

One chip processes packets on a number of independent channels
Packet processing is stateful: the output for a packet can depend on all previous input on the same channel.

Channel Separation Property in P-logic

Property of interest: channel separation ( = no information leaks between channels)

  ┌─────────┐   ┌─────────┐
──┤  chip   ├──►┤ pick ch ├──►
  └─────────┘   └─────────┘

  ┌─────────┐   ┌─────────┐
──┤ pick ch ├──►┤  chip   ├──►
  └─────────┘   └─────────┘

assert Separation = ∀ ch . {pick ch . chip} === {chip . pick ch} pick :: Channel → [Packet] → [Packet] pick ch = filter ((==ch).fst)

Alternative view of the Channel Separation Property

	┌──────┐
     ───┤ chip ├──►
        └──────┘

      ┌─────────┐   ┌─────────┐
   ┌─►┤ pick 1  ├──►┤  chip   ├──┐
   │  └─────────┘   └─────────┘  │
   │  ┌─────────┐   ┌─────────┐  │
───┼─►┤ pick 2  ├──►┤  chip   ├──┼──►
   │  └─────────┘   └─────────┘  │
   │      ...          ...       │
   │  ┌─────────┐   ┌─────────┐  │
   └─►┤ pick n  ├──►┤  chip   ├──┘
      └─────────┘   └─────────┘

Processing all channels in one chip is the same as having one chip per channel.

Filling in the details

This is the definition main Separation assertion:

chip :: Algs → ChipState → [Packet] → [Packet] type Algs = Channel → Alg type ChipState = (Memory,Regs) type Regs = FM RegFile assert Separation = ∀ algs . ∀ ch . ∀ state . ∀ ps . {pick ch (chip algs state ps)} === {chip algs state (pick ch ps)}

The Chip Model in Haskell, more details

chip :: Algs → ChipState → [Packet] → [Packet] chip algs state ps = fst (runS (manyPackets algs ps) state) manyPackets :: Algs → [Packet] → StateM ChipState [Packet] manyPackets algs = mapM (onePacket algs) onePacket :: Algs → Packet → StateM ChipState Packet onePacket algs (chan,ws) = do regfile ← liftM (\regs→FM.lookup regs chan) (inSnd load) (ws',regfile') ← inFst (doPacket (algs chan) ws regfile) finishPacket chan ws' regfile' doPacket :: Alg → Data → RegFile → StateM Memory (Data,RegFile) doPacket alg ws regf = ...

We get some separation by construction
Not visible above: memory protection...

For reference...

Generic monadic operations

liftM :: Monad m ⇒ (a → b) → m a → m b mapM :: Monad m ⇒ (a → m b) → [a] → m [b]

State monad operations

inFst :: StateM s1 a → StateM (s1,s2) a inSnd :: StateM s2 a → StateM (s1,s2) a runS :: StateM s a → s → (a,s)

An observation

Although the function chip is defined in a monadic style, it is equivalent(*) to a simple list traversing function:

chip algs state [] = [] chip algs state (p:ps) = p':chip algs state' ps where (p',state') = runS (onePacket algs p) state

Under the assumption that onePacket has the right properties, we can prove Separation with induction over the input packet list, without reasoning about monadic code.

(*) This equivalence follows directly from the definitions.

Overall proof structure

The proof of Separation is obtained by combining two the proofs of two main properties: CondSeparation and AllGoodAlgs.

assert CondSeparation = ∀ algs ch state1 state2 ps . GoodAlg {algs ch} ==> Invariant state1 state2 ch ==> {pick ch (chip algs state1 ps)} === {chip algs state2 (pick ch ps)}

assert AllGoodAlg = ∀ alg . GoodAlg alg

This factoring of the proof as some advantages...

Observations

Maintaining the Invariant makes sure that there is no information leaks through the register files.
GoodAlgs makes sure that there are no information leaks through the shared memory.
Thanks to the use of GoodAlgs as an assumption, the proof of CondSeparation is valid even if memory protection is removed from the chip. This opens up for some design choices...

CondSeparation proof outline

Base case, ps = []: trivial, because LHS = RHS = []
Induction step: ps = (ch',ws):ps'
- Two cases
  - ch' == ch: the equation reduces to
    - {p1:pick ch (chip algs state1' ps')} === {p2:chip algs state2' (pick ch ps')}
      This follows from follows from the invariant, GoodAlg (algs ch) and the induction hypothesis (using Invariant ch state1' state2').
      Seems to correspond to step consistency in [Rus92].
  - ch' /= ch: the equation reduces to
    - {pick ch (chip algs state1' ps')} === {chip algs state2 (pick ch ps')}
      This follows from the invariant and the induction hypothesis.
      Seems to correspond to local respect in [Rus92].

AllGoodAlg proof outline

The proof is done by structural decomposition.
- The basic operations preserve the invariant.
- The combinators produce results that preserve the invariant if the parts preserve the invariant.
The basic operations are reads and writes in the protected memory monad.
The combinators used include monadic combinators like, >>=, liftM and return.
The properties required of the combinators are essentially the free theorems for the respective types.
No monad laws needed to be proved or referenced explicitly.

Proof effort

a few days, for first simplified version
1-2 man weeks in total
- for whom?
- code written by someone else, not intimately familiar with it
- never tried to prove separation before, not an expert on security
- familiar with the programming language
- familiar with the proof tool

Proof size

Two main modules:

SeparationProof: 3-4 screen-fulls
proves CondSeparation (separation holds provided the observed channel algorithm is well-behaved)
GoodAlgProof: 3-4 screen-fulls
proves AllGoodAlgs (thanks to memory protection, all algorithms are well-behaved)
total proof file sizes in bytes: 23k+22k+... = 85k (11k compressed)
Total program+properties size in bytes: 14k (4.5k compressed)

Relevance to current work

Although designed to model hardware, the Chip Model can also be seen as a model of a simple operating system.
Channel separation corresponds to separation between processes.
The proof techniques outlined in this talk are likely to be applicable when proving separation properties for our microkernel implementation in Haskell.

A formal proof of the Chip Model Channel Separation Property

Thomas Hallgren, Talk at the Programatica Review Meeting, 2004-09-16

A formal proof of the Chip Model Channel Separation Property

Thomas Hallgren

Talk at the Programatica Review Meeting, 2004-09-16

The Chip

Proof of the separation property

The Chip Model in Haskell

Channel Separation Property in P-logic

Alternative view of the Channel Separation Property

Filling in the details

The Chip Model in Haskell, more details

For reference...

Generic monadic operations

State monad operations

An observation

Overall proof structure

Observations

CondSeparation proof outline

AllGoodAlg proof outline

Proof effort

Proof size

Relevance to current work

The End

Questions?

References